정다면체(오일러의 법칙)

안녕하세요~

제가 소개드릴 지식은 중학교 1학년 2학기 도형 부분에서 외워야만 한다고 생각했던 정다면체의 꼭짓점과 모서리의 수를 쉽게 계산을 통하여 구하는 방법입니다~

우선 정다면체란 모든 면이 합동인 정다각형으로 이루어지고, 각 꼭짓점에 모인 면의 개수가 같은 입체도형입니다.

정다면체는 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체의 다섯 가지 종류밖에 없다는 사실은 알고 계시겠죠? 이 때, 이름에서 나오는 정★면체의 ★은 면의 개수를 뜻하는 것이구요.

우선 입체도형이 되려면 적어도 세 개 이상의 면이 한 꼭짓점에 모여야 한다는 사실을 생각합니다. 두 개의 면이 모이면 단지 책처럼 펼쳐지는 평면 도형일 뿐이니까요.

정삼각형은 한 각의 크기가 60도입니다.

한 꼭짓점에 면이 3개, 4개, 5개까지밖에 모일 수 없는 이유는 한 꼭짓점에 6개의 면이 모이면 360도 즉 평면이 되기 때문입니다.

같은 이유로 정사각형, 정오각형은 한 꼭짓점에 3개의 면이 모인 도형 밖에는 나올 수 없고, 정육각형은 한 각의 크기가 120도이므로 세 개만 모여도 360도가 되기 때문에 정다면체를 만들 수 없습니다.

여기서 정삼각형이 한 꼭짓점에 3개 모인 도형을 정사면체, 4개 모인 도형을 정육면체, 5개 모인 도형을 정십이면체, 정사각형이 한 꼭짓점에 3개 모인 도형을 정육면체, 정오각형이 한 꼭짓점에 3개 모인 도형을 정십이면체라고 합니다.

그럼 본격적으로 꼭짓점의 수와 모서리의 수를 계산해 볼까요?

1) 정다면체의 꼭짓점의 수를 구하는 방법

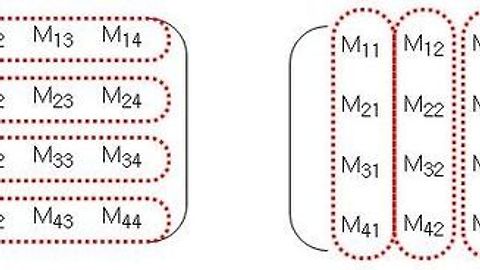
한 꼭짓점에 도형이 3개 모인다는 것은 한 꼭짓점을 이루기 위해서 정다각형의 꼭짓점 3개가 하나로 합쳐져야 한다는 것을 뜻합니다.

정사면체의 경우 정삼각형이 한 꼭짓점에 3개 모여있고, 각 면의 모양이 삼각형이므로 꼭짓점이 3개인 도형이 4개 있으니 꼭짓점의 전체 수는 3X4=12개이고, 이 때, 꼭짓점이 3개씩 모여 한 꼭짓점을 이루므로 12를 3으로 나누어 4개가 됩니다.

정육면체의 경우 정사각형이 6개이고, 한 꼭짓점에 3개의 면이 모여 있으므로 같은 방법으로 4X6을 3으로 나눈 8이 되는 것이지요.

이를 공식으로 정리하면

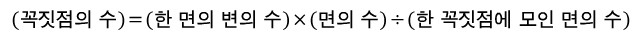
가 되겠네요.

2) 정다면체의 모서리의 수를 구하는 방법

입체도형의 모든 모서리는 2개의 변이 모여 이루어집니다. 무조건 2개의 변이 합쳐져 1개의 모서리를 이루는 것입니다.

정사면체의 경우 정삼각형이 4개이고, 2개의 변이 하나로 합쳐지게 되므로 3X4를 2로 나누어 6개이고, 정육면체의 경우 정사각형이 6개이고, 2개의 변이 하나로 합쳐지게 되므로 4X6을 2로 나누면 12개가 되겠네요.

이를 공식으로 정리하면

가 됩니다.

이렇게 원리를 이해하면 어렵게 암기하지 않고도 정다면체의 꼭짓점이나 모서리의 수를 쉽게 구할 수 있겠지요?\

그림으로 보고 이해하자.

점선면으로 개수 구하기

정다면체의 점의 개수, 선의 개수, 면의 개수를 세서,
(점의 개수) - (선의 개수)+ (면의 개수)의 값을 계산해 보면,
어떤 정다면체인가에 관계없이 2가 됨.