삼각함수 구현

1. 삼각함수의 구현 이해
 

우리가 프로그래밍을 하면서 자주 사용하는 여러 수학 함수들이 있다. 할일 없는 사람들은 이 함수들이 어떻게 작동하는지 정말 궁금해할지도 모른다.  한 번 내가 알고 있는 것들을 글로 써보며 생각을 정리해보고자 한다.

수학함수를 구현할때 가장 중요한 점은 정밀도와 속도이다.
늘상 있는 일이지만 프로그래머는 정확성과 속도 사이를 잘 조율해야한다. 필요이상의 정밀도는 시간 낭비일뿐이다.

삼각함수는 비용이 비싼 측에 낀다. (계산량을 줄일만한 획기적 방법이 별로 없는듯하다.) 그래서 삼각함수 연산을 자주 하는 프로그램에서는 대게 테이블을 만들어놓고 참조하는 방법을 쓴다. 이 방법이 대체로 빠른 방법이어서 추천하는 바이다. (가장 좋은 방법은 FPU의 빵빵한 지원이라고나 할까) 아래에 설명하는 계산법은 그냥 이렇게도 계산할수 있다는 거지, 이 식을 활용해서 계산하면 좋다는 의미는 아니다.

공학용으로 삼각함수계산을 어떻게 하나 궁금해서 영어위키백과를 찾아봤더니, 부정확하지만 빠른 오일러 방법을 이용하는 경우도 있고, 정밀한 근사를 위해 체비쇼프 근사나 Padé 근사를 이용하는 경우도 있었지만, 너무 어려운걸 설명하면 머리아프므로(사실 필자가 머리가 아프다.) 그냥 쉬운 걸로만 선택해서 설명하겠다.

2. 삼각함수를 코드로 구현을 해보았습니다.
 
//범위는 -PI ~ PI 로 둡니다.

double Sine(double x)
{

      double sum = x;
      double result = x;
      double fact = 1.0f;
      double x2 = x*x*-1.0f;;

 

      //유한한 테일러 급수 전개
      for(int i=1;i<9;++i)
      {
            fact *= ((2*i) * (2*i+1));
            result *= x2;
            sum += (result / fact);
      }

      return sum;
}

 

원리는, 함수의 테일러 전개에 있습니다.

 

위에서 예를 든, sin함수의 테일러 전개는

 

 

 

 

 

 

 

 

 

 

 

 

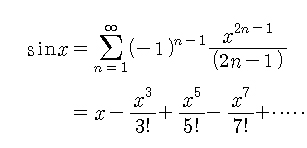
입니다.

 

단순히 이 공식을 제한해서 적용한 것 뿐이죠.

 

shader 1.x 에서는 보통, 상수레지스터 하나에 들어갈 수 있는 값이 4개(xyzw)이기 때문에 n=4 까지만 해줍니다.

 

위에선 sin 함수만을 예로 들었는데, cos 함수도 마찬가지로 테일러 전개를 이용해서 함수를 작성해주면 됩니다.

 
출저: